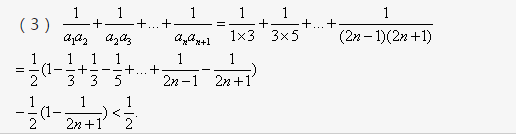| 更多

【高中数学】学会这几种方法，数列不难 2015-05-29 17:01:00　阅读 次 参与讨论()马上投稿

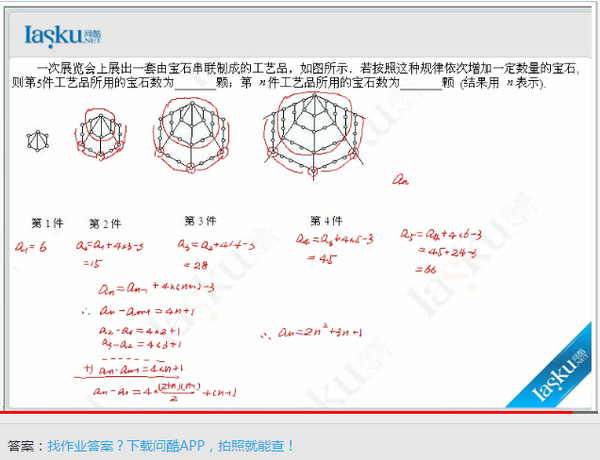
　　近几年来，高考关于数列方面的命题主要有以下三个方面：

　　（1）数列本身的有关知识，其中有等差数列与等比数列的概念、性质、通项公式及求和公式。

　　（2）数列与其它知识的结合，其中有数列与函数、方程、不等式、三角、几何的结合。

　　（3）数列的应用问题，其中主要是以增长率问题为主。

　　试题的难度有三个层次，小题多以基础题为主，解答题多以基础题和中档题为主，只有个别地方用数列与几何的综合与函数、不等式的综合作为最后一题，难度较大。

　　接下来为大家介绍下高中数列解题中，经常会用到的几种方法，大家可以按照这个解题思路来回答数列相关的问题（以下例题均来自于问酷网，超全的中小学在线学习互动平台，找题目，就上问酷网www.iasku.com）。掌握了这几点并融会贯通，你会发现，数列其实并不难。

　　（1）函数的思想方法

　　数列本身就是一个特殊的函数，而且是离散的函数，因此在解题过程中，尤其在遇到等差数列与等比数列这两类特殊的数列时，可以将它们看成一个函数，进而运用函数的性质和特点来解决问题。

　　（2）方程的思想方法

　　数列这一章涉及了多个关于首项、末项、项数、公差、公比、第n项和前n项和这些量的数学公式，而公式本身就是一个等式，因此，在求这些数学量的过程中，可将它们看成相应的已知量和未知数，通过公式建立关于求未知量的方程，可以使解题变得清晰、明了，而且简化了解题过程。

　　示例>>

　　解析>>

　　更多解题拓展可点击进入问酷网，还能看解题视频哦！

　　（3）不完全归纳法

　　不完全归纳法不但可以培养学生的数学直观，而且可以帮助学生有效的解决问题，在等差数列以及等比数列通项公式推导的过程就用到了不完全归纳法。

　　（4）倒序相加法

　　等差数列前n项和公式的推导过程中，就根据等差数列的特点，很好的应用了倒序相加法，而且在这一章的很多问题都直接或间接地用到了这种方法。

　　示例>>

　　更多解题拓展可点击进入问酷网，查看解题视频！

　　（5）错位相减法

　　错位相减法是另一类数列求和的方法，它主要应用于求和的项之间通过一定的变形可以相互转化，并且是多个数求和的问题。等比数列的前n项和公式的推导就用到了这种思想方法。

　　这里使用了两式相减的方法：

　　解析>>