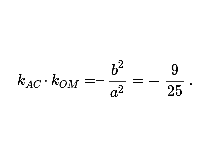【方法技巧】一般圆锥曲线的“垂径定理”2015-07-20 13:45:00 阅读 次 参与讨论()马上投稿
已知某椭圆的焦点是F1(-4,0),F2(4,0),过点F2并垂直于x轴的直线与椭圆的一个交点为B,且|F1B|+|F2B|=10.椭圆上不同的两点A(x1,y1),C(x2,y2)满足条件:|F2A|、|F2B|、|F2C|成等差数列.
(1) 求该椭圆的方程;
(2) 求弦AC中点的横坐标;
(3) 设弦AC的垂直平分线的方程为y=k
|
已知某椭圆的焦点是F1(-4,0),F2(4,0),过点F2并垂直于x轴的直线与椭圆的一个交点为B,且|F1B|+|F2B|=10.椭圆上不同的两点A(x1,y1),C(x2,y2)满足条件:|F2A|、|F2B|、|F2C|成等差数列. (1) 求该椭圆的方程; (2) 求弦AC中点的横坐标; (3) 设弦AC的垂直平分线的方程为y=kx+m,求m的取值范围.
值得注意的是,不仅圆、椭圆、双曲线这些有心二次曲线有“垂径定理”,双曲线的两条渐近线 x2/a2-y2/b2 = 0 作为退化的双曲线,也有与双曲线相似的“垂径定理”.下题(2014年浙江理16)就是很经典的一例: |
相关资源:
网友评论
网站最近动态
云南省玉溪第一中学2025-2026学年高一上学期开学考试(新)
云南省玉溪第一中学2025-2026学年高一上学期开学考试(新)
辽宁省普通高中2024-2025学年高二下学期期中考试
河北省保定市示范高中2025届高三下学期5月质量检测试题
高考资源网(www.ks5u.com),您身边的高考专家!