| 更多

喜讯：2015年高考真题——理科数学（新课标Ⅰ卷）第18题 命中12分2015-07-02 10:59:00　阅读 次 参与讨论()马上投稿

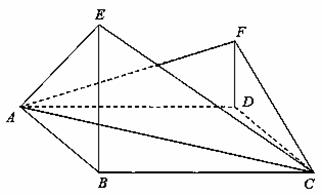
喜讯：2015年高考真题——理科数学（新课标Ⅰ卷）第18题 命中12分

      高考真题：2015年高考真题——理科数学（新课标Ⅰ卷）

      http://www.ks5u.com/down/2015-6/7/1772716.shtml

【高考真题】如图，，四边形ABCD为菱形，∠ABC=120°，E，F是平面ABCD同一侧的两点，BE⊥平面ABCD，DF⊥平面ABCD，BE=2DF，AE⊥EC.

（Ⅰ）证明：平面AEC⊥平面AFC

（Ⅱ）求直线AE与直线CF所成角的余弦值

【答案】（Ⅰ）略（Ⅱ）

【命中试题】：【江苏省宿迁市2015届高三上学期第一次摸底考试数学试题 第22题】

http://www.ks5u.com/down/2014-12/11/1557241.shtml

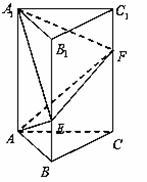
如图，在直三棱柱中，已知，，，点，分别在棱，上，且，，．

（1）当时，求异面直线与所成角的大小；

（2）当直线与平面所成角的正弦值为时，求的值．

【答案】（1）（2）．

、

【命中试题】：【Ks5u首发】湖南省益阳市2015届高三4月调研考试 数学（理） 第19题】

http://www.ks5u.com/down/2015-4/10/1710780.shtml

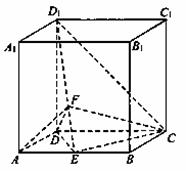
（本小题满分12分）如图，在长方体ABCD-A₁B₁C₁D₁中，AA₁=AB=2AD=2，E为AB的中点，F为D₁E上的一点，D₁F=2FE．

（Ⅰ）证明：平面平面；

（Ⅱ）求二面角的平面角的余弦值．

【答案】（Ⅰ）略（Ⅱ）．

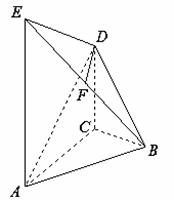
【命中试题】：【江西省鹰潭市2015届高三第一次模拟考试理科数学试题 第19题】

http://www.ks5u.com/down/2015-4/11/1711348.shtml

在如图所示的几何体中，平面，∥，是的中点，，，．

（1）证明平面；

（2）求二面角的余弦值的大小．

【答案】（1）略；（2）；

【命中试题】：【Ks5u解析】天津市南开区2015届高三一模考试数学文试题 第17题】

http://www.ks5u.com/down/2015-5/8/1742233.shtml

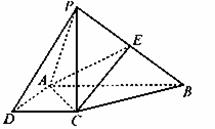
如图，在四棱锥P-ABCD中，四边形ABCD是直角梯形，AB⊥AD，AB∥CD，PC⊥底面ABCD，AB=2AD=2CD=4，PC=2a，E是PB的中点．

（Ⅰ）求证：平面EAC⊥平面PBC；

（Ⅱ）若二面角P-AC-E的余弦值为，求直线PA与平面EAC所成角的正弦值．

【答案】（Ⅰ）略；（Ⅱ）．

【命中试题】：【广东省深圳市2015届高三第二次调研考试数学理试题 第18题】

http://www.ks5u.com/down/2015-4/25/1727466.shtml

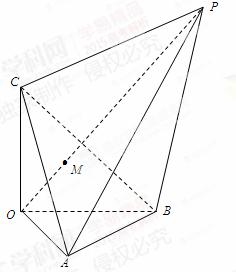
如图，已知三棱锥的三条侧棱，，两两垂直，△为等边三角形， 为△内部一点，点在的延长线上，且．

（1）证明：；

（2）证明：平面平面；

（3）若，，求二面角的余弦值．

【答案】（1）略  （2）略  （3）