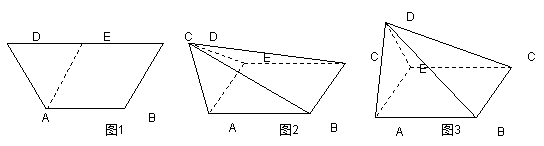
喜讯：2017年高考资源网压轴卷全国卷数学命中209分

高考试题全国卷Ⅰ理科数学18题100%来自押题卷

【高考真题1】2017年高考真题——数学（全国卷Ⅰ）理科18题/文科18题（命中12+6分）

（12分）如图，在四棱锥中，中，且．
            
（1）证明：平面平面；
（2）若，，求二面角的余弦值．

【命中试题】KS5U2017全国卷Ⅰ高考压轴卷  数学（理）第19题

如图1，等腰梯形中，。取线段中点，将沿折起，如图2所示。（Ⅰ）当平面折到与底面所成的二面角为时，如图3所示，求此时二面角平面角的余弦值。

命题解析--图形构造完全一致，所求二面角完全一致。解题思路均为利用空间向量。

高考真题所给的条件PA=PD＝AB＝DC，命中题的条件DA＝DE＝AB=CE。

【高考真题2】2017年高考真题——数学（文）（全国卷Ⅱ）16题命中原题5分

16.△ABC的内角A,B,C的对边分别为a,b,c,若2bcosB=acosC+ccosA,则B=       

【命中试题】 KS5U2017全国卷Ⅲ高考压轴卷  数学（文）第17题

已知的内角，，的对边分别为，，，若，，且.求角的值

解析：由题意只  2bcosA=acosC+ccosA

命题解析：高考真题与押题均考察解三角形的知识，本题的切入点为射影定理

注acosC+ccosA=b（射影定理结论）

【高考真题3】 2017年高考真题——数学（理）（全国卷Ⅲ）第20题解析几何命中12分

20．（12分）已知抛物线C：y²=2x，过点（2,0）的直线l交C与A,B两点，圆M是以线段AB为直径的圆。（1）证明：坐标原点O在圆M上；

（2）设圆M过点，求直线l与圆M的方程。

【命中试题】：KS5U2017全国卷Ⅰ高考压轴卷 数学（理）第20题

已知点,是抛物线上的两个动点,是坐标原点,向量,满足.设圆的方程为

(I) 证明线段是圆的直径;

命题分析与解题揭秘：命题背景与题干

高考真题：题干过（２，０）抛物线上两点AB，AB是圆M的直径，证明坐标原点O在圆M上：只需证明OA⊥OB

压轴卷：AB是抛物线上两个动点，且，还有一个圆的等式，证明AB是圆C的直径。只需要证明O在圆M上

【高考真题4】2017年高考真题——数学（全国卷Ⅰ）理科13题命中5分

已知向量，的夹角为，，，则________．

【命中试题】KS5U2017全国卷3高考压轴卷 数学（理） 第13题

已知平面向量a，b满足|a|＝，|b|＝2，a·b＝－3，则|a＋2b|＝

命题解析：均为向量的基本运算考察，切入点所给条件完全一致，所求内容完全一致。

题干中所给的，的夹角为可以求出a·b的值为1，本题所要求得内容完全一致！

北京卷高考7题，新课标2卷14题来源自新课标压轴卷2—取材100%一样命中10分

【高考真题5】2017年高考真题——数学（理）（北京卷）第7题  命中5分

（7）某四棱锥的三视图如图所示，则该四棱锥的最长棱的长度为

（A）3（B）2（C）2（D）2

【命中试题】：KS5U2017全国卷Ⅱ高考压轴卷  数学（文） 第9题

四棱锥的三视图如图所示，其五个顶点都在同一球面上，若四棱锥的侧面积等于,则该外接球的表面积是

(A)  (B)       (C)      (D)

命题揭示：两者的取材均为四棱椎，押题卷上的题所给条件稍复杂。根据侧面积可以计算出图中的棱长为a=2，四棱锥完全一致，在设问方面高考真题所求为最长的棱长，最长的棱长为对角线，最长的棱长为正方体的对角线，，命中题中，所求为球的表面积，球的半径（为对角线的一半，对角线的长也为2）。在这题的考察中，全国卷中也出现了类似题目

【高考真题6】2017年高考真题——数学（理）（全国卷Ⅲ） 第21题 命中12分

已知函数。

（1）若，求a的值；

（2）设m为整数，且对于任意正整数n，求m的最小值。

试题分析：(1)由原函数与导函数的关系可得x=a是在的唯一最小值点，列方程解得；

(2)利用题意结合(1)的结论对不等式进行放缩，求得，结合可知实数的最小值为

【命中试题】： KS5U2017全国卷Ⅲ高考压轴卷 数学（理）第10题，

KS5U2017全国卷Ⅰ高考压轴卷 数学（理）第11题

已知是定义在上的奇函数，且时，，则函数（为自然对数的底数）的零点个数是（）

函数有，所以函数在上单调递增，在上单调递减，当时函数有极大值为

数列{a_n}的通项公式为an=，关于{a_n}有如下命题：

P1：{a_n}为先减后增数列；P2：{a_n}为递减数列；

P3：P4：其中正确的是

命中分析：第一个直接命中lnx-x+1，第二个乃高考题的本质题根，利用放缩，利用第一问所证明得到的结论，两边取对数题根证明：

以下为命中的相似度较高的真题，仅仅数据不同，其他完全一致的试题

函数图像部分命中15分

【高考真题7】2017年高考真题——数学（文）（全国卷Ⅰ） 第8题 命中5分,

.函数的部分图像大致为（）

【命中试题】KS5U2017全国卷Ⅲ高考压轴卷 数学（文）第8题

命题解析：同为考察奇函数偶函数的复合函数的奇偶性，还有三角函数奇偶性的考察

【高考真题8】 2017年高考真题——数学（理）（全国卷Ⅰ）第5题—命中5分

函数在单调递减，且为奇函数．若，则满足的的取值范围是（）
A．                      B．                      C．                    D．

【命中试题】：KS5U2017全国卷Ⅰ高考压轴卷 数学（文） 第5题

已知函数，则下列不等式中正确的是（）

A．             B．     C．D．

命题解析：两者均考察了奇函数的性质，通过奇函数的单调性解决不等式问题，突破点，解题思路完全一致，可作为姊妹题。

高考题：因为为奇函数，所以，于是等价于|又在单调递减

命中题：函数为奇函数，又在上递增，所以

为奇函数，又是递增函数，由得，，从而

【高考真题9】：2017年高考真题——数学（理）（北京卷）第6题 命中5分

已知函数，则

         （A）是奇函数，且在R上是增函数  （B）是偶函数，且在R上是增函数

         （C）是奇函数，且在R上是减函数  （D）是偶函数，且在R上是减函数

【命中试题】：KS5U2017全国卷Ⅱ高考压轴卷 数学（文）第6题

下列函数中，与函数的奇偶性、单调性均相同的是（）

考察内容完全一致，100%相似，仅仅数据不同，考点完全一样

概率部分

【高考真题10】2017年高考真题——数学（文）（全国卷Ⅱ）第11题 命中5分

从分别写有1,2,3,4,5的5张卡片中随机抽取1张，放回后再随机抽取1张，则抽得的第一张卡片上的数大于第二张卡片上的数的概率为

A.B.C.D.

【命中试题】：KS5U2017全国卷Ⅲ高考压轴卷 数学（文） 第5题

袋中有五张卡片，其中红色卡片三张，标号分别为，蓝色卡片两张，标号分别为，从以上五张卡片中任取两张，则这两张卡片颜色不同且标号之和不小于的概率为

（A）（B）（C）（D）

命题分析：问题背景考察方式一致，以抽卡片为背景考察概率知识

三角函数函数性质

【高考真题11】：2017年高考真题——数学（文）（全国卷Ⅲ）第6题命中5分

设函数f(x)=cos(x+)，则下列结论错误的是

A．f(x)的一个周期为−2π                            B．y=f(x)的图像关于直线x=对称

C．f(x+π)的一个零点为x=           D．f(x)在(,π)单调递减

【命中试题】：KS5U2017全国卷Ⅲ高考压轴卷 数学（文）第7题

已知函数, 则函数的图象

A. 关于直线对称                    B. 关于点直线对称

C. 最小正周期为T=2p                     D. 在区间上为减函数

命题方式-命题意图-所给函数-所给选项完全一致，三角函数的对称性，周期性及单调性的考查

复数命中5分

【高考真题12】：2017年高考真题——数学（文）（全国卷Ⅲ）第2题命中5分

复平面内表示复数z=i(-2+i)的点位于

A.第一象限               B.第二象限               C.第三象限               D.第四象限

【命中试题】：KS5U2017全国卷Ⅱ高考压轴卷  数学（文）第2题

已知（是虚数单位），那么复数z对应的点位于复平面内的

       （A）第一象限             （B）第二象限            （C）第三象限        （D）第四象限

考察：复数的意义及运算，命题完全一致

二项式展开式的通项公式命中5分

【高考真题13】：：2017年高考真题——数学（理）（全国卷Ⅲ）第6题

的展开式中³³的系数为

A．                                B．                             C．40                                   D．80

【命中试题】：KS5U2017全国卷1高考压轴卷 数学（理）第13题

的展开式中的系数为。

命题分析：所给的题干略微差别，所求的内容完全一致

数列命中5分

【高考真题14】：2017年高考真题——数学（理）（全国卷Ⅲ）第14题：

设等比数列满足a₁ + a₂ = –1, a₁ – a₃ = –3，则a₄ = _。

考察等比数列的性质

【命中试题】：KS5U2017全国卷Ⅱ高考压轴卷 数学（文）第5题

已知为等比数列，，，则（）