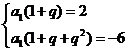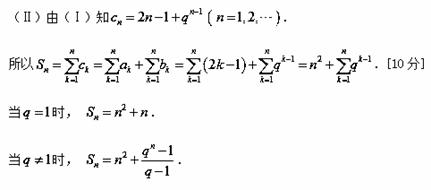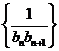喜讯:2017年高考真题——数学(文)(全国卷Ⅰ)第17题命中63分2017-06-28 09:02:00 阅读 次 参与讨论()
|
喜讯:2017年高考真题——数学(文)(全国卷Ⅰ) 集合的基本运算 (命中63 分) 【高考真题】2017年高考真题——数学(文)(全国卷I)第17题 12分 记Sn为等比数列 (1)求 (2)求Sn,并判断Sn+1,Sn,Sn+2是否成等差数列. 【解】(1)设 故 (2)由(1)可得 由于 故
【命中试题一】 陕西省汉中市2017届高三下学期第二次教学质量检测(4月模拟)数学(文)试题 Word版含答案 /down/2017-4/12/2642589.shtml
7.《张丘建算经》是我国南北朝时期的一部重要数学著作,书中系统的介绍了等差数列,同类结果在三百多年后的印度才首次出现。书中有这样一个问题,大意为:某女子善于织布,后一天比前一天织得快,而且每天增加的数量相同,已知第一天织布尺,一个月(按30天计算)总共织布 A.尺 B. 【答案】B
【命中试题二】安徽省阜阳市2017届高三第二次质量检测数学文科试卷 Word版含答案 /down/2017-4/18/2652145.shtml 3.等比数列 A. 【答案】D
【命中试题三】《KS5U首发》湖南省娄底市2017届高考仿真模拟(二模)数学(文)试题 Word版含答案 /down/2017-4/19/2655291.shtml 9.南北朝时期我国数学著作《张丘建算经》有一道题为:“今有十等人,每等一人,宫赐金以等次差降之,上三人先入,的金四斤,持出,下四人后入得金三斤,持出,中间三人未到者,亦依等次更给,问各得金几何?”则在该问题中,等级较高的二等人所得黄金比等级较低的八等人和九等人两人所得黄金之和 A. 多 【答案】D
【命中试题四】重庆市2017届高三4月调研测试(二诊)数学文试题 Word版含答案 /down/2017-4/16/2649669.shtml 5. 《张丘建算经》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有女不善织,日减功迟,初日织五尺,末日织一尺,今共织九十尺,问织几日?”,已知“日减功迟”的具体含义是每天比前一天少织同样多的布,则此问题的答案是( ) A.10日 B. 20日 C. 30日 D.40日 【答案】B
【命中试题五】四川省资阳市2017届高三4月模拟考试数学(文)试题 Word版含答案 /down/2017-4/9/2637498.shtml 2.已知等差数列 (A) 2 (B) 3 (C) 4 (D) 5 【答案】A
【命中试题六】安徽省马鞍山市2017届高三第三次模拟数学(文)试卷 Word版含答案 /down/2017-5/8/2682090.shtml 17.已知数列 (Ⅰ)求 (Ⅱ)设 【答案】(1)
【命中试题七】北京市西城区2017届高三5月模拟测试(二模)数学文试卷 17.设 (Ⅰ)若 (Ⅱ)求数列 【答案】(1)
【命中试题八】《KS5U解析》四川省泸州市2017届高三数学四诊试卷(文科) Word版含解析 /down/2017-6/21/2757306.shtml 17.已知数列 (1)求数列 (2)设 【答案】(1)
【命中试题九】《KS5U首发》福建省三明市2017届高三下学期5月质量检查 数学(文) Word版含答案 17.(本小题满分12分) 已知数列 (Ⅰ)求数列 (Ⅱ)设 【答案】(I)
|