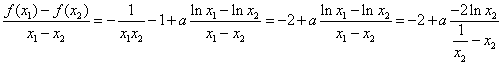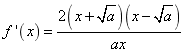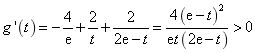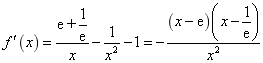喜讯:2018年高考真题——理科数学(全国卷I)第21题 共命中24分2018-07-03 11:43:00 阅读 次 参与讨论()
|
喜讯:2018年高考真题——数学(理)(全国卷I)第21题 函数的单调性 (命中24分)
【高考真题】2018年高考真题——数学(理)(全国卷I)第21题 24分 https://www.ks5u.com/down/2018-6/8/3242892.shtml 21.(12分) 已知函数 (1)讨论 (2)若 【答案】解:(1) (i)若 (ii)若 当 当 (2)由(1)知, 由于 所以 设函数 所以 【命中试题一】 2018年全国统一考试最新高考信息卷(九) 第21题 https://www.ks5u.com/down/2018-5/25/3219769.shtml 21.(12分)已知函数 (1)讨论函数 (2)若函数 【答案】(1)当 【解析】(1) 当 当 知 (2)由(1)知, 依题意 由 由 欲证 注意到 只要证明 由 所以 令 则 【命中试题二】 2018年普通高校全国统一考试仿真卷(二) 第21题 https://www.ks5u.com/down/2018-4/5/3136691.shtml 21.已知函数 (1)讨论函数 (2)证明: 【答案】(1) 【解析】(1) 所以 (2)由(1)可知当 对于任意 ① 即 ②当 所以 所以 所以 综合①②可知,所求实数 |
网友评论
安徽省县中联盟2025-2026学年高一上学期10月联考试题
安徽省县中联盟2025-2026学年高一上学期10月联考试题
江浙皖高中(县中)发展共同体2025-2026学年高三上学期10月联考试题
江浙皖高中(县中)发展共同体2025-2026学年高三上学期10月联考试题