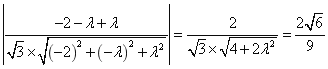| 更多

喜讯：2018年高考真题——理科数学（全国卷I）第18题 共命中36分2018-07-03 11:49:00　阅读 次 参与讨论()

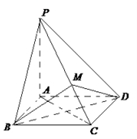
https://www.ks5u.com/down/2018-6/8/3242892.shtml 

18．（12分）

如图，四边形为正方形，分别为的中点，以为折痕把折起，使点到达点的位置，且.

（1）证明：平面平面；

（2）求与平面所成角的正弦值.

【答案】解：（1）由已知可得，BF⊥PF，BF⊥EF，所以BF⊥平面PEF.

又平面ABFD，所以平面PEF⊥平面ABFD.

（2）作PH⊥EF，垂足为H.由（1）得，PH⊥平面ABFD.

以H为坐标原点，的方向为y轴正方向，为单位长，建立如图所示的空间直角坐标系H−xyz.

由（1）可得，DE⊥PE.又DP=2，DE=1，所以PE=.又PF=1，EF=2，故PE⊥PF.

可得.

则为平面ABFD的法向量.

设DP与平面ABFD所成角为，则.

所以DP与平面ABFD所成角的正弦值为.

【命中试题一】 2018年全国统一考试最新高考信息卷（九） 第18题

           https://www.ks5u.com/down/2018-5/25/3219769.shtml

18．（12分）如图，在四棱锥中，四边形为正方形，平面，，是上一点，且．

（1）求证：平面；

（2）求直线与平面所成角的正弦值．

【答案】（1）证明见解析；（2）．

【解析】（1）连接，由平面，平面得，

又，，∴平面，得，

又，，∴平面．

（2）法1：由（1）知平面，即是直线与平面所成角，易证，而，

不妨设，则，，，

在中，由射影定理得，

可得，所以，

故直线与平面所成角的正弦值为．

法2：取为原点，直线，，分别为，，轴，建立坐标系，不妨设，则，，，

由（1）知平面得法向量，而，

∴，

故直线与平面所成角的正弦值为．

【命中试题二】 2018年全国统一考试最新高考信息卷（七） 第19题

          https://www.ks5u.com/down/2018-5/25/3219725.shtml

19．（12分）如图，在四棱锥中，底面，，，，，．

（1）求证：平面平面；

（2）若棱上存在一点，使得二面角的余弦值为，求与平面所成角的正弦值．

答案】（1）见解析；（2）．

【解析】（1）证明：，，

，

平面，平面，

，

，

平面，

平面，

平面平面．

        https://www.ks5u.com/down/2018-4/5/3136693.shtml

19．棱台的三视图与直观图如图所示．

（1）求证：平面平面；

（2）在线段上是否存在一点，使与平面所成的角的正弦值为？若存在，指出点的位置，若不存在，说明理由．

【答案】（1）见解析；（2）点在的中点位置，理由见解析．

【解析】（1）根据三视图可知平面，为正方形，

所以．········1分

因为平面，所以，········2分

又因为，所以平面．········4分

因为平面，所以平面平面．········5分

（2）以为坐标原点，，，所在直线分别为，，轴建立空间直角坐标系，如图所示，

根据三视图可知为边长为2的正方形，为边长为1的正方形，

平面，且．

所以，，，，．

因为在上，所以可设．

因为，

所以．

所以，········7分

．········8分

设平面的法向量为，

根据，

令，可得，所以．········9分

设与平面所成的角为，

所以．

所以，即点在的中点位置