| 更多

喜讯：2018年高考真题——数学（理）（天津卷）第16题命中26 分2018-07-05 09:17:00　阅读 次 参与讨论()

喜讯：2018年高考真题——数学（理）（天津卷）

概率

（命中26 分）

【高考真题】2018年高考真题——数学（理）（天津卷）第16题  13分

    /down/2018-6/9/3244269.shtml

已知某单位甲、乙、丙三个部门的员工人数分别为24，16，16. 现采用分层抽样的方法从中抽取7人，进行睡眠时间的调查.

（I）应从甲、乙、丙三个部门的员工中分别抽取多少人？

（II）若抽出的7人中有4人睡眠不足，3人睡眠充足，现从这7人中随机抽取3人做进一步的身体检查.

（i）用X表示抽取的3人中睡眠不足的员工人数，求随机变量X的分布列与数学期望；

 （ii）设A为事件“抽取的3人中，既有睡眠充足的员工，也有睡眠不足的员工”，求事件A发生的概率.

【答案】（Ⅰ）解：由已知，甲、乙、丙三个部门的员工人数之比为3∶2∶2，由于采用分层抽样的方法从中抽取7人，因此应从甲、乙、丙三个部门的员工中分别抽取3人，2人，2人．

（Ⅱ）（i）解：随机变量X的所有可能取值为0，1，2，3．P（X=k）=（k=0，1，2，3）．所以，随机变量X的分布列为

随机变量X的数学期望．

（ii）解：设事件B为“抽取的3人中，睡眠充足的员工有1人，睡眠不足的员工有2人”；事件C为“抽取的3人中，睡眠充足的员工有2人，睡眠不足的员工有1人”，则A=B∪C，且B与C互斥，由（i）知，P(B)=P(X=2)，P(C)=P(X=1)，故P(A)=P(B∪C)=P(X=2)+P(X=1)=．所以，事件A发生的概率为．

【命中试题一】北京市昌平临川育人学校2018届高三下学期期中考试数学（理）试题 Word版含答案

/down/2018-4/27/3169168.shtml

18.  从高一年级随机选取100名学生，对他们期中考试的数学和语文成绩进行分析，成绩如图所示.

（Ⅰ）从这100名学生中随机选取一人，

求该生数学和语文成绩均低于60分的概率;

（Ⅱ）从语文成绩大于80分的学生中随机选取两人，

记这两人中数学成绩高于80分的人数为，

求的分布列和数学期望;

（Ⅲ）试判断这100名学生数学成绩的方差与

语文成绩的方差的大小.（只需写出结论）

【答案】（Ⅰ）由图知有9名学生数学和语文成绩均低于60分,则从100名学生中随机选一人,该生数学和语文成绩均低于60分的概率为.

（Ⅱ）由题可知,的可能取值为0,1,2

（Ⅲ）

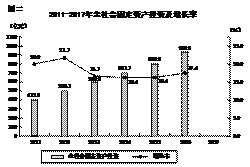
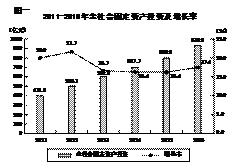
【命中试题二】北京市通州区2018届高三数学（理）一模考试试题 Word版含答案/down/2018-5/2/3175277.shtml

16. 作为北京副中心，通州区的建设不仅成为京津冀协同发展战略的关键节点，也肩负着医治北京市“大城市病”的历史重任，因此，通州区的发展备受瞩目. 2017年12月25日发布的《北京市通州区统计年鉴（2017）》显示：2016年通州区全区完成全社会固定资产投资939.9 亿元，比上年增长17.4％，下面给出的是通州区2011-2016年全社会固定资产投资及增长率，如图一.

又根据通州区统计局2018年1月25日发布：2017年通州区全区完成全社会固定资产投资1054.5亿元，比上年增长12.2％. 

（Ⅰ）在图二中画出2017年通州区全区完成全社会固定资产投资（柱状图），标出增长率并补全折线图；

（Ⅱ）通过计算2011-2017这7年的平均增长率约为17.2％，现从2011-2017这7年中随机选取2个年份，记为“选取的2个年份中，增长率高于17.2％的年份个数”，求的分布列及数学期望；

（Ⅲ）设2011-2017这7年全社会固定资产投资总额的中位数为，平均数为，比较与的大小（只需写出结论）.

【答案】解：（Ⅰ）

…

（Ⅱ）依题意，的可能取值为，，.                   

，，.    所以的分布列为