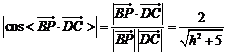| 更多

喜讯：2018年高考真题——数学（理）（天津卷）第17题命中26分2018-07-05 09:19:00　阅读 次 参与讨论()

喜讯：2018年高考真题——数学（理）（天津卷）

立体几何

（命中26 分）

【高考真题】2018年高考真题——数学（理）（天津卷）第17题  13分

    /down/2018-6/9/3244269.shtml

如图，且AD=2BC，,且EG=AD，且CD=2FG，，DA=DC=DG=2.

（I）若M为CF的中点，N为EG的中点，求证：；

（II）求二面角的正弦值；KS5U

（III）若点P在线段DG上，且直线BP与平面ADGE所成的角为60°，求线段DP的长.

【答案】依题意，可以建立以D为原点，分别以，，的方向为x轴，y轴，z轴的正方向的空间直角坐标系（如图），可得D（0，0，0），A（2，0，0），B（1，2，0），C（0，2，0），E（2，0，2），F（0，1，2），G（0，0，2），M（0，，1），N（1，0，2）．

（Ⅰ）证明：依题意=（0，2，0），=（2，0，2）．设n₀=(x，y，z)为平面CDE的法向量，则 即 不妨令z=–1，可得n₀=（1，0，–1）．又=（1，，1），可得，又因为直线MN平面CDE，所以MN∥平面CDE．

（Ⅱ）解：依题意，可得=（–1，0，0），，=（0，–1，2）．

设n=（x，y，z）为平面BCE的法向量，则 即 不妨令z=1，可得n=（0，1，1）．

设m=（x，y，z）为平面BCF的法向量，则 即 不妨令z=1，可得m=（0，2，1）．

因此有cos<m，n>=，于是sin<m，n>=．

所以，二面角E–BC–F的正弦值为．

（Ⅲ）解：设线段DP的长为h（h∈［0，2］），则点P的坐标为（0，0，h），可得．

易知，=（0，2，0）为平面ADGE的一个法向量，故，

由题意，可得=sin60°=，解得h=∈［0，2］．所以线段的长为.

【命中试题一】北京市朝阳区2018届高三二模数学（理）试题

/down/2018-5/7/3185353.shtml

17.如图，在四棱锥中，平面平面.是等腰三角形，且.在梯形中，，，，，

（1）求证：平面；

（2）求二面角的余弦值；

（3）在线段上是否存在点，使得平面？请说明理由.

【命中试题二】北京市通州区2018届高三数学（理）一模考试试题 Word版含答案/down/2018-5/2/3175277.shtml

17. 如图所示的几何体中，平面平面,为等腰直角三角形， ，四边形为直角梯形，，，，，. 

（Ⅰ）求证：平面；

（Ⅱ）求二面角的余弦值；

（Ⅲ）在线段上是否存在点，使得

平面，若存在，求的值；若不存在，请说明理由. 

【答案】解：（Ⅰ）因为，，所以四边形是平行四边形. 所以因为平面，平面， 所以平面      

（Ⅱ）取的中点为，因为，所以 因为平面平面,平面，所以平面                                      

以点为坐标原点，分别以直线，为轴，轴建立空间直角坐标系，则轴在平面内． 因为，，，

所以，，，，

所以，.   设平面的法向量为，所以  即所以 令，则，. 

所以.      设平面的法向量为，所以又因为二面角为锐角，所以二面角的余弦值是     

（Ⅲ）存在. 设点，，所以，所以， ， .    所以点所以又平面的法向量为，平面，所以所以

所以在线段上存在点，使平面，且的值是