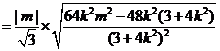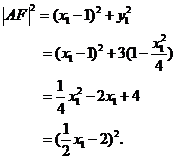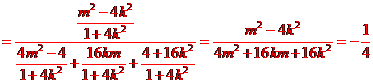| 更多

喜讯：2018年高考真题——数学（理）（天津卷）第19题命中26分2018-07-05 09:22:00　阅读 次 参与讨论()

喜讯：2018年高考真题——数学（理）（天津卷）

解析几何

（命中26 分）

【高考真题】2018年高考真题——数学（理）（天津卷）第19题  13分

    /down/2018-6/9/3244269.shtml

设椭圆(a>b>0)的左焦点为F，上顶点为B. 已知椭圆的离心率为，点A的坐标为，且.

（I）求椭圆的方程；

（II）设直线l：与椭圆在第一象限的交点为P，且l与直线AB交于点Q.

若(O为原点) ，求k的值.

【答案】（Ⅰ）解：设椭圆的焦距为2c，由已知知，又由a²=b²+c²，可得2a=3b．由已知可得，，，由，可得ab=6，从而a=3，b=2．

所以，椭圆的方程为．

（Ⅱ）解：设点P的坐标为（x₁，y₁），点Q的坐标为（x₂，y₂）．由已知有y₁>y₂>0，故．又因为，而∠OAB=，故．由，可得5y₁=9y₂．

由方程组消去x，可得．易知直线AB的方程为x+y–2=0，由方程组

消去x，可得．由5y₁=9y₂，可得5（k+1）=，两边平方，整理得，解得，或．

所以，k的值为

【命中试题一】北京市东城区2018年高三文科数学综合练习（二）（二模）试卷 Word版含答案

/down/2018-5/9/3190184.shtml

20. 已知椭圆的右焦点为，离心率为．

（Ⅰ）求椭圆的方程；

（Ⅱ）是椭圆在轴右侧部分上的两个动点，若原点到直线的距离为，证明：△的周长为定值．

【答案】（Ⅰ）由题意得   解得     所以椭圆的方程为．

（Ⅱ）①当垂直于轴时，方程为，      ，，．       ．       因为，

 所以．                         

②当不垂直于轴时，设的方程为．因为原点到直线的距离为，所以，即．          

由得，

即．

设，，则，．

所以

             ．                             

因为,在轴右侧，所以，所以．

          所以，同理．                                   

所以．

所以．

综上，△的周长等于椭圆的长轴长．    

【命中试题二】北京市昌平临川育人学校2018届高三下学期期中考试数学（理）试题 Word版含答案

/down/2018-4/27/3169168.shtml

20.已知椭圆的离心率为，且过点．

（Ⅰ）求椭圆的方程；

（Ⅱ）设，是椭圆上不同于点的两点，且直线，的斜率之积等于，

试问直线是否过定点？若是，求出该点的坐标；若不是，请说明理由．

【答案】解:（Ⅰ），，过，，，

，

（Ⅱ）①当斜率不存在时，设，则，

，，

又在椭圆上，，解得，，．

②当斜率存在时，设，与椭圆联立，由

得，，即，

设，，

则，，[来源:Zxxk.Com]

，

，，或，

当时，，恒过不符合①，

当时，，结合①，恒过，

综上，直线恒过．