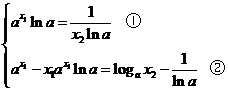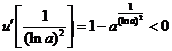喜讯:2018年高考真题——数学(理)(天津卷)第20题命中14分2018-07-05 09:25:00 阅读 次 参与讨论()
|
喜讯:2018年高考真题——数学(理)(天津卷) 导数 (命中14 分) 【高考真题】2018年高考真题——数学(理)(天津卷)第20题 14分 /down/2018-6/9/3244269.shtml 已知函数 (I)求函数 (II)若曲线 (III)证明当 【答案】(I)解:由已知, 令 由a>1,可知当x变化时,
所以函数 (II)证明:由 由 因为这两条切线平行,故有 两边取以a为底的对数,得 (III)证明:曲线 曲线 要证明当 即只需证明当 由①得 因此,只需证明当 设函数 由此可得 所以 下面证明存在实数t,使得 当 所以,当 【命中试题一】北京市东城区2018年高三文科数学综合练习(二)(二模)试卷 Word版含答案 (Ⅰ)当 (Ⅱ)若直线 【答案】解: (Ⅰ)当 所以 令 因为
所以
(Ⅱ)因为 设直线 所以 又因为 即 所以 设 因为 所以 所以 |
网友评论
北京市西城区2024-2025学年高一下学期期末考试
山西省晋中市部分学校2025-2026学年高一上学期11月质量检测试题
山西省晋中市部分学校2025-2026学年高一上学期11月质量检测试题