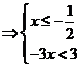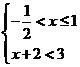喜讯：2019年高考真题——理科数学（全国I卷）第23题（命中20分）2019/7/9 15:52:00　阅读 次 参与讨论()

喜讯：2019年高考真题——理科数学（全国卷Ⅰ）

不等式证明

（命中20分）

【高考真题】2019年高考真题——理科数学（全国卷Ⅰ）第23题  10分

https://www.ks5u.com/down/2019-6/9/3700679.shtml

23．[选修4—5：不等式选讲]（10分）

已知a，b，c为正数，且满足abc=1．证明：

（1）；

（2）．

23．解：（1）因为，又，故有

.

所以.

（2）因为为正数且，故有

=24.

所以.

【命中试题1】

《KS5U发布》江苏省苏锡常镇四市2019届高三第三次模拟考试 数学

http://www.ks5u.com/down/2019-5/14/3670426.shtml

21C. (选修45：不等式选讲)

已知正数a，b，c满足a＋b＋c＝2，求证：＋＋≥1.

【答案】21C. 证明：因为a>0，b>0，c>0，a＋b＋c＝2，由柯西不等式，得

[(b＋c)＋(c＋a)＋(a＋b)](＋＋)

＝[()²＋()²＋()²][()²＋()²＋()²]

＝(＋＋)²(5分)

＝(a＋b＋c)²＝2²，(8分)

则＋＋≥＝＝1.

所以＋＋≥1.(10分)

【命中试题2】

《Ks5u发布》四川省攀枝花市2019届高三第二次统一考试数学（理）试卷 Word版含答案

http://www.ks5u.com/down/2019-4/8/3613647.shtml

23.[选修4 — 5:不等式选讲]（10分）

    已知 a>0，b>0，，

求证：(I) ；

      (II) 。

【答案】23.（本小题满分10分）选修4-5：不等式选讲解：

（Ⅰ）由

或或

或或

所以函数的定义域为．………………5分

（Ⅱ）法一：

因为，所以，．

故，即

所以．………………10分

法二：当时，  ∴，

∴，即 ，

∴．………………10分