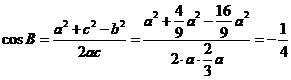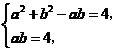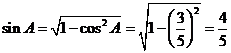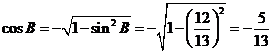喜讯：2019年高考真题——文科数学（天津卷）

解三角形

（命中65分）

【高考真题】2019年高考真题——文科数学（天津卷） 第16题  13分

https://www.ks5u.com/down/2019-6/9/3700663.shtml

（16）（本小题满分13分）

在中，内角所对的边分别为.已知，.

（Ⅰ）求的值；

（Ⅱ）求的值.

（16）本小题主要考查同角三角函数的基本关系，两角和的正弦公式，二倍角的正弦与余弦公式，以及正弦定理、余弦定理等基础知识.考查运算求解能力.满分13分.

（1）解：在中，由正弦定理，得，又由，得，即.又因为，得到，.由余弦定理可得

.

（Ⅱ）解：由（1）可得，从而，，故.

【命中试题1】

《Ks5u发布》重庆市第一中学2019届高三下学期4月模拟考试 数学（文）

http://www.ks5u.com/down/2019-5/28/3691829.shtml

17.（本小题满分12分）中，内角对应的边分别为，满足.

（Ⅰ）已知求与的值；

（Ⅱ）若且求.

【答案】17.解：，因为，且，

所以，所以..……………（4分）

（Ⅰ）因为，，所以

，

....……………（6分）

由正弦定理知：，即..……………（8分）

（Ⅱ）因为，所以，所以，所以..……（12分）

【命中试题2】

《Ks5u发布》天津市河西区2019届高三下学期总复习质量调查（二）数学（文）试题（二模） Word版含答案

http://www.ks5u.com/down/2019-5/6/3649823.shtml

（16）（本小题满分13分）

在中，，，对应的边为，，.

（Ⅰ）若，，且的面积等于，求和，的值；

（Ⅱ）若是钝角，且，，求的值.

【答案】（16）本小满分13分.

（Ⅰ）解：因为,,所以.

所以.          

由余弦定理及已知条件得，，             

又因为的面积等于，所以，得． 

联立方程组   解得，．  ……………………7分

（Ⅱ）解：因为是钝角，且，.

所以                                          

    所以                      

     ………………13分  

【命中试题3】《KS5U发布》江苏省苏锡常镇四市2019届高三第三次模拟考试 数学

http://www.ks5u.com/down/2019-5/14/3670426.shtml

16. (本小题满分14分)

在△ABC中，角A，B，C的对边分别为a，b，c，且＝.

(1) 求角A的大小；

(2) 若cos(B＋)＝，求cos C的值．

【答案】16. 解：(1) 由正弦定理＝＝，且＝，(1分)

得＝，(2分)

则有sin A＝2－cos A，即sin A＋cos A＝2，2sin(A＋)＝2，

故sin(A＋)＝1.(4分)

因为A∈(0，π)，则A＋∈(，)，所以A＋＝，即A＝.(6分)

(2) 在△ABC中，因为A＝，则B∈(0，)，B＋∈(，)，所以sin(B＋)>0.

因为cos(B＋)＝，所以sin(B＋)＝＝.(8分)

在△ABC中，A＋B＋C＝π，(9分)

所以cos C＝cos(π－A－B)＝－cos(A＋B)＝－cos(B＋)(10分)

＝－cos[(B＋)＋]＝－cos(B＋)cos ＋sin(B＋)sin

＝－×＋×＝.(14分)

【命中试题4】《KS5U发布》江苏省七市（南通、泰州、扬州、徐州、淮安、宿迁、连云港）2019届高三第三次调研考试 数学 Word版

http://www.ks5u.com/down/2019-5/13/3668908.shtml

15. (本小题满分14分)

在△ABC中，a，b，c分别为角A，B，C所对边的长，a(sin A－sin B)＝(c－b)(sin B＋sin C)．

(1) 求角C的值；

(2) 若a＝4b，求sin B的值．

【答案】15. 解：(1) 在△ABC中， 因为a(sin A－sin B)＝(c－b)(sin B＋sin C)，

由正弦定理＝＝，

所以a(a－b)＝(b＋c)(c－b)，(3分)

即a²＋b²－c²＝ab.

由余弦定理c²＝a²＋b²－2abcos C，得cos C＝.(5分)

因为0<C<π，所以C＝.(7分)

(2) (解法1)因为a＝4b及a²＋b²－c²＝ab，

得c²＝16b²＋b²－4b²＝13b²，即c＝b.(10分)

由正弦定理＝，得＝，所以sin B＝.(14分)

(解法2)由正弦定理＝，得sin A＝4sin B.

由A＋B＋C＝π，得sin(B＋C)＝4sin B.

因为C＝，所以sin B＋cos B＝4sin B，即7sin B＝cos B．(11分)

因为sin²B＋cos²B＝1，解得sin²B＝.

在△ABC中，因为sin B>0，所以sin B＝.(14分)

【命中试题5】《KS5U发布》2019年相阳教育“黉门云”高考等值试卷★预测卷（全国I卷） 数学（文） Word版含答案

http://www.ks5u.com/down/2019-5/14/3669965.shtml

17．（12分）已知△ABC中，为钝角，而且，，AB边上的高为．

（1）求的大小；

（2）求的值．

【答案】17．（12分） （1）由三角形面积可知

，

………………………………2分

，又因为是锐角，所以．

………………………………5分

（2）由（1）可知

，

所以．

………………………………7分

又因为

，

………………………………9分

因此

．

………………………………12分