一、选择题(本大题共6小题,每小题7分,共42分)
1. 函数f(x)=x3+3x2+3x-a的极值点的个数为 ( )
a.0 b.1 c.2 d.3
解析:f′(x)=3x2+6x+3=3(x+1)2≥0恒成立.所以f(x)在r上单调递增,故f(x)无极值.
答案:a
2.已知函数y=f(x),其导函数y=f′(x)的图象如图所示,则y=f(x) ( )
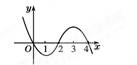
a.在(-∞,0)上为减函数 b.在x=0处取极小值
c.在(4,+∞)上为减函数 d.在x=2处取极大值
解析:使导函数y=f′(x)>0的x的取值范围为增区间;使导函数y=f′(x)<0的x的取值范围为减区间.
答案:c
3. 已知函数f(x)的定义域为(0,+∞),且f(x)>0,f′(x)>0,那么函数y=xf(x) ( )
a.存在极大值 b.存在极小值
c.是增函数 d.是减函数
解析:y′=f(x)+xf′(x)>0,x∈(0,+∞),所以选c.
答案:c
4.函数y=x3-2ax+a在(0,1)内有极小值,则a的取值范围是 ( )
资源难易程度:★★★★★★★★★★★★★★★
高考资源网版权所有 ©2005-2010
未经许可,盗用或转载本站资料者,本站将追究其法律责任!