命题方向 单利计算问题
［例1］ 有一种零存整取的储蓄项目，它是每月某日存入一笔相同的金额，这是零存；到一定时期到期，可以提出全部本金及利息，这是整取.它的本利和公式如下：
本利和=每期存入金额×［存期+
存期×(存期+1)×利率］.
(1)试解释这个本利公式.
(2)若每月初存入100元，月利率5.1‰，到第12月底的本利和是多少？
(3)若每月初存入一笔金额，月利率是5.1‰，希望到第12个月底取得本利和2000元，那么每月应存入多少金额？
［分析］ 存款储蓄是单利计息，若存入金额为a，月利率为p，则n个月后的利息是nap.
［解析］ (1)设每期存入金额a，每期利率p，存入期数为n，则各期利息之和为
ap+2ap+3ap+…+nap=n(n+1)ap.
连同本金，就得：本利和=na+n(n+1)ap=a［n+n(n+1)p］.
(2)当a=100,p=5.1‰,n=12时，
本利和=100×（12+×12×13×5.1‰）=1239.78(元).
(3)将(1)中公式变形得
a=
=
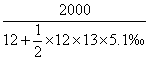≈161.32(元).
资源难易程度:★★★★★★★★★★★★★★★
高考资源网版权所有 ©2005-2014
未经许可，盗用或转载本站资料者，本站将追究其法律责任！
