1.（本小题满分14分）已知函数
.
(1) 试证函数
的图象关于点
对称;
(2) 若数列
的通项公式为
, 求数列的前m项和
(3) 设数列
满足: 
, 
. 设
.
若(2)中的
满足对任意不小于2的正整数n, 
恒成立, 试求m的最大值.
解: (1)设点
是函数的图象上任意一点, 其关于点的对称点为
.
由
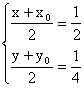得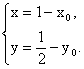
所以, 点p的坐标为p
.………………(2分)
由点在函数的图象上, 得
.
∵
∴点p在函数的图象上.
∴函数的图象关于点对称. ………………(4分)
(2)由(1)可知, 
, 所以
,
即
………………(6分)
由
, ……………… ①
得
………………②
由①＋②, 得
∴
………………(8分)
(3) ∵
, ………………③
∴对任意的
. ………………④
由③、④, 得
即
.
∴
.……………(10分)
∵
∴数列是单调递增数列.
∴
关于n递增. 当
, 且
时, 
.
∵
∴
………………(12分)
∴
即
∴
∴m的最大值为6. ……………(14分)
资源难易程度:★★★★★★★★★★★★★★★
高考资源网版权所有 ©2005-2014
未经许可，盗用或转载本站资料者，本站将追究其法律责任！
