1．（本小题满分12分）
过抛物线
上不同两点a、b分别作抛物线的切线相交于p点，
（1）求点p的轨迹方程；
（2）已知点f（0，1），是否存在实数
使得
？若存在，求出的值，若不存在，请说明理由.
解法（一）：（1）设
由
得：
………………………………3分
直线pa的方程是：
即
①
同理，直线pb的方程是：
②
由①②得：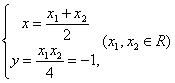
∴点p的轨迹方程是
……………………………………6分
（2）由（1）得：
…………………………10分
所以
故存在=1使得…………………………………………12分
解法（二）：（1）∵直线pa、pb与抛物线相切，且
∴直线pa、pb的斜率均存在且不为0，且
设pa的直线方程是
由
得：
即
…………………………3分
即直线pa的方程是：
同理可得直线pb的方程是：
由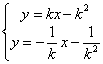
得：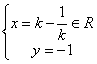
故点p的轨迹方程是……………………………………6分
（2）由（1）得：
………………………………10分
故存在=1使得…………………………………………12分
资源难易程度:★★★★★★★★★★★★★★★
高考资源网版权所有 ©2005-2014
未经许可，盗用或转载本站资料者，本站将追究其法律责任！
