1．（本小题满分14分）
设抛物线
的焦点为f，动点p在直线
上运动，过p作抛物线c的两条切线pa、pb，且与抛物线c分别相切于a、b两点.
（1）求△apb的重心g的轨迹方程.
（2）证明∠pfa=∠pfb.
解：（1）设切点a、b坐标分别为
，
∴切线ap的方程为：
切线bp的方程为：
解得p点的坐标为：
所以△apb的重心g的坐标为 
，
所以
，由点p在直线l上运动，从而得到重心g的轨迹方程为：
（2）方法1：因为
由于p点在抛物线外，则
∴
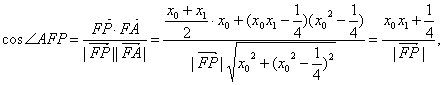
同理有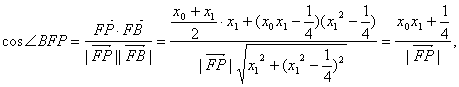
∴∠afp=∠pfb.
方法2：①当
所以p点坐标为
，则p点到直线af的距离为：
即
所以p点到直线bf的距离为：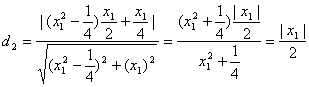
所以d1=d2，即得∠afp=∠pfb.
②当
时，直线af的方程：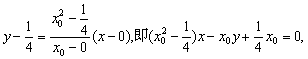
直线bf的方程：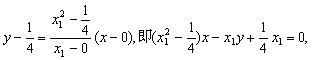
所以p点到直线af的距离为：
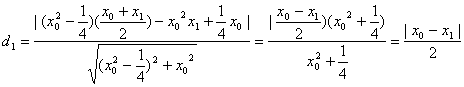，同理可得到p点到直线bf的距离
，因此由d1=d2，可得到∠afp=∠pfb.
资源难易程度:★★★★★★★★★★★★★★★
高考资源网版权所有 ©2005-2014
未经许可，盗用或转载本站资料者，本站将追究其法律责任！
