一般性数学试卷的最后一题在测试学生的数学素养的基础上,本着适度区分的原则,最后一题的三个小题的坡度逐渐提升,达到分层的效果.这些试题一般性取材于课本但高于课本,强调知识的灵活运用,综合性较强,原创题较少,大多属于改编体,它们的基本图形在几何画板中加以研究,达到推陈出新的效果,绝大多数属于改编题.下面以08年静安、杨浦两区模拟考最后一题为例,进行归纳分析.它们的难度略低于中考的压轴题.
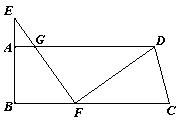 例1.(08静安)如图,在四边形ABC D中,∠B=90°,AD//BC,AB=4,BC=12,点E在边BA的延长线上,AE=2,点F在BC边上,EF与边AD相交于点G,DF⊥EF,设AG=x, DF=y.
例1.(08静安)如图,在四边形ABC D中,∠B=90°,AD//BC,AB=4,BC=12,点E在边BA的延长线上,AE=2,点F在BC边上,EF与边AD相交于点G,DF⊥EF,设AG=x, DF=y.
(1)求y关于x的函数解析式,并写出定义域;
(2)当AD=11时,求AG的长;
(3)如果半径为EG的⊙E与半径为FD的
⊙F相切,求这两个圆的半径.
分析:本题以直角梯形为载体,第1小题梯形结合相似形知识来研究两条线段的数量关系,探求函数关系式和定义域;第2小题在研究特殊情况下知道函数值AD=11求自变量AG的值,第三小题结合圆的内容以两圆相切(外切和内切)这一知识点来压轴.其实如果学生基础扎实,利用两圆相切关系建立等式:当⊙E与⊙F外切时,EF=EG+FD=EG+FG,当⊙E与⊙F内切时,EF= FD–EG,相关的量都用含自便量的代数式来表示,从而利用关系等式建立方程,解方程求出自便量的值,再求出两个圆的半径,考察了方程思想.
高考资源网版权所有 ©2005-2009
未经许可,盗用或转载本站资料者,本站将追究其法律责任!